مکانیک سیالات

مکانیک سیالات

مکانیک سیالات یکی از دروس  مهم در دوره کاردانی صنایع شیمیایی میباشد 

که در زیر به نکتهای کلیدی این درس که در دوره کاردانی اساتیدتاکید بیشتری

به آنها دارند اشاره میکنم (بر گرفته از مکانیک سیالات شیمز)

انواع سیالات

سیال تراکم‌ناپذیر

در بررسی انواع مختلف سیالاتی که تحت شرایط استاتیکی قرار دارند، پی می‌بریم که بعضی از سیالات ، علی‌رغم وجود فشارهای زیاد ، تغییرات چگالی بسیار کمی ‌دارند. حالت مایع بودن این سیالات به خاطر همین رفتار است. تحت چنین حالتی ، سیال را تراکم‌ناپذیر می‌نامند و در ضمن محاسبات فرض می‌کنند چگالی آن ثابت است. مطالعه سیالات تراکم‌ناپذیر را در شرایط استاتیکی ، هیدرولیک می‌نامند.

سیال تراکم‌پذیر

در جایی که چگالی را تحت شرایط استاتیکی نتوان ثابت گرفت، مانند یک گاز ، سیال را تراکم‌پذیر می‌گویند و برای مشخص کردن این دسته از مسائل اغلب از نام آئروستاتیک بهره می‌گیریم. این طبقه‌بندی از لحاظ تراکم‌پذیری ، در محدوده علم استاتیک صورت می‌گیرد. در دینامیک سیالات ، اینکه چه وقت می‌توان چگالی را ثابت گرفت، تنها به نوع سیال بستگی ندارد.

حرکات انواع سیالات

حرکت سیال غیریکنواخت

از آنجا که سیال نمی‌تواند بدون حرکت در برابر تنش برشی مقاومت کند، سیال ساکن لزوما باید بطور کامل از تنش فارغ باشد. سیالی که حرکت یکنواخت دارد، یعنی جریانی که در آن سرعت تمام اجزا یکسان است، نیز فارغ از تنش برشی است، زیرا تغییر سرعت در تمام جهتها در جریان یکنواخت باید صفر باشد ( v/∂n=0∂).

حرکت سیال غیرچسبناک

سیالی را که چسبناکی آن از لحاظ نظری صفر است، سیال غیرچسبناک می‌گویند. از آنجا که قسمت اعظم جریانها ، آثار چسبناکی ناچیز و قابل صرفنظری دارند، لذا ایده‌آل‌سازی و ساده‌سازی‌های ناشی از آن را اغلب به خوبی می‌توان بهره گرفت. قانون حرکت نیوتن را برای یک جرم منشوری بینهایت کوچک سیال در داخل جریان می‌توان بکار برد.

حرکت سیال چسبناک

آثار چسبناکی را در نظر می‌گیریم، البته معنی‌اش این است که تنشهای برشی حضور دارند، یعنی 9 تنش غیر صفر وارد به سه وجه متعامد در یک نقطه ، می‌تواند وجود داشته باشد. برای اینکه تنش در یک نقطه را مورد بحث قرار دهیم، بهتر است که یک چهاروجهی بینهایت کوچک از سیال را بررسی کنیم. 9 تنش بر وجه عقبی چهاروجهی وارد می‌آید. با بکارگیری قوانین حرکت نیوتن در جهت عمود بر سطح مایل چهار وجهی ، تنش برشی را می‌توان برحسب 9 تنش قائم بر صفحات مرجع بدست آورد.

تغییر فشار در یک سیال

برای توزیع فشار در سیالات ، تعادل نیروهای وارد بر یک جز بینهایت کوچک سیال را در نظر می‌گیریم. نیروهای وارد بر این جز از فشار محیط اطراف و نیروی گرانشی ناشی می‌شوند. اگر فشار فقط در جهت محور z باشد که برخلاف جهت شتاب جاذبه گرانشی (ثقل) انتخاب شده است، می‌تواند تغییر کند. از آنجا که P فقط در جهت z تغییر می‌کند و تابعی از x و y نیست، از معادله زیر می‌توان استفاده کرد:

dP/dz=-γ

این معادله دیفرانسیل برای هر سیال استاتیک تراکم‌پذیر واقع در یک میدان گرانشی صادق است. برای ارزیابی خود توزیع فشار ، بین دو حد که بطور متناسب انتخاب شده اند، با انتگرالگیری از رابطه فوق خواهیم داشت:

P-P_atm=γ(z-z₀)=γd

که در آن d عبارت است از فاصله زیر سطح آزاد. P-P_atm یعنی فشار بالای فشار جو را ، فشار نسبی (پیمانه‌ای) می‌گوییم.

تغییر فشار با ارتفاع در یک سیال استاتیک تراکم‌پذیر

فواصل عمومی‌ گازها در مسائل فشارسنجی کوچک هستند و در نتیجه برای این گازها از تغییر فشار با ارتفاع چشم پوشی می‌کنیم، ولی در محاسباتی که با فاصله‌های عمومی ‌بزرگ سروکار دارند، مانند مسائل مربوط به جو سیارات ، اغلب باید تغییر فشار گاز با ارتفاع را در نظر بگیریم. با مراجعه به معادله دیفرانسیل dP/dz = -γ که فشار ، وزن مخصوص و ارتفاع را به هم ارتباط می‌دهد، اکنون فرض می‌کنیم، γ یک متغیر است و به این ترتیب تاثیرهای تراکم‌پذیری را امکان‌پذیر می‌کند. خودمان را به گاز کامل محدود می‌کنیم که این فرض برای هوا و اکثر عناصر آن در گسترده نسبتا وسیعی از فشار و دما صحت دارد. (g/V=γ)

حالت اول

اگر گاز کامل تکدما باشد، در این حالت ، معادله حالت گاز نشان می‌دهد که حاصلضرب PV ثابت است. بدین ترتیب ، در هر مکان داخل سیال با استفاده از اندیس 1 که داده‌های معلوم را نشان می‌دهد، می‌توان نوشت:

PV=P₁V₁=Cte

 

(P=P₁exp(-γ₁(z-z₁)/P₁

 

حالت دوم

اگر دما با ارتفاع بطور خطی تغییر ‌کند، تغییر دما برای این حالت به صورت زیر است:

T=T₁+kz

که در آن T₁ عبارت است از دما در داده (z=0) که آن را اغلب آهنگ افت می‌نامند و ثابت است. در مسائل زمینی k منفی خواهد بود. برای اینکه بتوانیم متغییرهای معادله dP/dz=-γ را جدا کنیم، باید γ را از معادله حالت بدست آوریم و در نهایت خواهیم داشت:

P=P₁(T₁/(T₁+kz))^g/kR

 

استاتیک شاره‌ها

در این مبحث ، شاره‌ها را همانطور که معمولا درک می‌شوند، تعریف می‌کنیم و تنها به خواصی از شاره‌ها می‌پردازیم که به توانایی جاری شدن آنها مربوط می‌شوند. بنابراین ، علی‌رغم اختلافهایی که در فشارهای معمولی بین مایعات و گازها مشاهده می‌شود، قوانین اساسی یکسانی بر رفتار استاتیک و دینامیک آنها حاکم می‌باشد. برای جامدات که اندازه و شکل معینی دارند، مکانیک اجسام صلب را می‌توان فرمولبندی کرد و آن را در مورد اجسامی ‌که نمی‌توان کاملا صلب فرضشان کرد، به کمک قوانین کشسانی اصلاح کرد.

چون شکل شاره‌ها به آسانی تغییر می‌کند و نیز حجم گازها مساوی با حجم ظرفی است که در آن قرار دارند، برای حل مکانیک شاره‌ها باید روشهای جدیدی بوجود آوریم. کاربرد مکانیک در مورد محیطهای پیوسته یعنی در جامدات و هم شاره‌ها ، بر قوانین حرکت نیوتن که با قوانین نیروی مناسبی ترکیب شده‌اند، مبتنی است. اما برای سهولت بهتر است در مورد شاره‌ها نیز مانند جامدات ، این قوانین اساسی را به صورت خاصی فرمولبندی کنیم.

تغییر فشار در یک شاره ساکن

هرگاه شاره‌ای در حال تعادل باشد، هر جز آن در حال تعادل خواهد بود. اگر عنصر حجمی‌ کوچکی از شاره را که در داخل شاره غوطه‌ور است، در نظر بگیریم و فرض کنیم که این عنصر به شکل یک قرص نازک است که به فاصله y بالاتر از یک سطح مرجع قرار گرفته است. ضخامت قرص dy و مساحت قاعده آن A است. جرم این عنصر ρAdy و وزن آن ρgdy است. نیروهای وارد بر عنصر ، از طرف شاره‌ای که آن را احاطه کرده است، در هر نقطه بر سطح عنصر عمودند. برآیند نیروهای افقی صفر است، زیرا این هیچ شتاب افقیی ندارد.

نیروهای افقی فقط از فشار شاره ناشی می‌شوند و به علت تقارن ، فشار در تمام نقاط واقع بر یک صفحه افقی در ارتفاع y یکسان است. عنصر شاره در راستای قائم نیز شتاب ندارد، یعنی برآیند نیروهای قائم وارد بر آن صفر است، اما نیروهای قائم نه تنها از فشار شاره بر وجه‌های عنصر بلکه از وزن عنصر نیز ناشی می‌شوند. اگر p فشار وارد بر وجه پایینی باشد و p+dp فشار وارد بر وجه بالایی باشد، نیروی رو به بالا pA است (که بر وجه پایینی وارد می‌شود) و نیروی رو به پایین که بر وجه بالایی وارد می‌شود، برابر است با (p+dp)A به اضافه وزن عنصر (dw) پس خواهیم داشت:

dp/dy=-ρg

 

دینامیک شاره‌ها

یکی از راههای توصیف حرکت یک شاره این است که آن را به عنصرهای حجمی ‌بی‌نهایت کوچک ، که می‌توان آنها را «ذره – شاره» نامید، تقسیم کنیم و به بررسی حرکت هر یک از این ذره‌ها بپردازیم که این کار دشواری است. به هر ذره – شاره مختصات x , y , z نسبت داده می‌شود که می‌توان آنها را توسط تابعهای x(x₀ , y₀ , z₀ , t₀ , t) , y(x₀ , y₀ , z₀ , t₀ , t) , z(x₀ , y₀ , z₀ , t₀ , t) که شاره را توصیف می‌کنند، تعیین کرد. این روش تعمیم مستقیمی ‌از مفاهیم مکانیک ذره‌ای است که نخستین بار توسط ژوزف لویی لاگرانژ (J.L.Lagrange) بکار گرفته شد.

روش دیگری نیز وجود دارد که توسط لئونارد اولر ارائه شده و برای بیشتر موارد مناسبتر است. در این روش به چگونگی گذشته هر ذره شاره توجهی نمی‌شود و در عوض چگالی و سرعت لحظه‌ای شاره را در هر نقطه با مشخص کردن چگالی (ρ(x,y,z,t و سرعت (V(x,y,z,t در نقطه (x,y,z) و در لحظه t بیان می‌کند. هر کمیتی (مانند فشار p) که در تعریف حالت شاره بکار برده شود، در هر نقطه از فضا و در هر لحظه از زمان دارای مقدار معینی خواهد بود. گرچه در این تعریف ، به جای یک ذره – شاره ، به یک نقطه فضا توجه می‌شود.
حالات ماده

دید کلی

یونانیان باستان ، عالم را متشکل از چهار عنصر آتش ، خاک ، آب و هوا می‌دانستند. امروزه دانشمندان بکمک این عناصر ، تمام اجزای تشکیل دهنده جهان را آن طور که هست ، توضیح می‌دهند. آتش بیانگر انرژی بوده و سه عنصر دیگر نشان دهنده سه حالت از ماده جامد ، مایع و گاز) می‌باشند. بر طبق این تقسیم بندی ، مواد جامد دارای شکل و ابعاد مشخصی بوده و همچنین جرم ، حجم و وزن مشخصی دارند.

مایعات و گازها شاره هستند، یعنی جریان می‌یابند. این اجسام شکل معینی ندارند و شکل ظرفی را که در آن قرار دارند بخود می‌گیرند، در حالیکه مقدار معینی دارند. مثلا مقدار آب ، دی اکسید کربن ، هوا ، شیر و غیره جرم قابل اندازه گیری و معینی دارند، اما نمی‌توانند همانند جامدات با اعمال نیروی پس زنی کشانی ، در مقابل تغییر شکل ، مقاومت کنند.

آزمایشات ساده

• مقدار معینی مایع ، حجم مشخصی دارد، گاز چنین نیست. اگر یک لیتر شیر را در چهار لیوان بریزیم، در مجموع همان یک لیتر حجم را اشغال می‌کند. حجم اشغال شده توسط سطح افقی بالای شیر در لیوان مشخص می‌شود. همین سطح است که باعث تمایز مایعات از گازها می‌شود.
  
  
• اگر گاز سنگین و قابل روئیت (رنگی) کلر را از ظرفی به ظرف دیگر بریزیم و در ظرف را باز بگذاریم ، گاز درون ظرف باقی نمی‌ماند. گازها همانند مایعات ، سطح افقی در بالای حجم اشغال کرده خود ندارند و در همه جا پخش می‌شوند. بنابراین ، حجم گاز برابرحجم هر ظرفی است که در آن قرار می‌گیرد.

جامد

در حالت جامد ، نیروهای بین مولکولی ، بقدری قویتر از انرژی جنبشی هستند که باعث سخت شدن جسم در نتیجه عدم جاری شدن آن می‌گردند. جامدات شکل و حجم معینی دارند. در جامدات فاصله مولکولها مانند فاصله آنها در مایع است. جامدات نمی‌توانند مانند وضعیتی که حالات مایع و گاز دارند، آزادانه به اطراف حرکت کنند. بلکه ، در جامد ، مولکولها در مکانهای خاصی قرار می‌گیرند و فقط می‌توانند در اطراف این مکانها حرکت نوسانی رفت و برگشتی بسیار کوچک انجام دهند.

این حرکت نوسانی ، بخصوص در جامدات بلورین ، کاربردهای صنعتی و علمی زیادی را برای این دسته از مواد به دنبال دارد.

مایع

در حالت مایع ، مولکولها بهم نزدیک‌تر بوده، بطوریکه نیروهای مابینشان قویتر از انرژی جنبشی آنان می‌باشد. از طرف دیگر ، نیروها آنقدر قوی نیستند که قادر به ممانعت از حرکت مولکولها گردند. از این روست که جریان مایع از ظرفی به ظرف دیگر شدنی است، اما نسبت سرعت جاری شدن آب در مقایسه با مایعات دیگر از قبیل روغنها و گلسیرین بسیار متفاوت است که این تفاوت در سرعت جاری شدن ، میزان مقاومت یک مایع در مقابل جاری شدن ،یعنی ویسکوزیته آن خوانده می شود که خود تابعی از شکل ، اندازه مولکولی ، درجه حرارت و فشار می‌باشد. بنابراین مایعات حجم معین و شکل نامعینی دارند.

فاصله مولکولها در مایعات در مقایسه با گازها بسیار کم است. در مایعات ، مولکولها به اطراف خود حرکت می‌کنند و به سهولت روی هم می‌لغزند و راحت جریان (شارش) پیدا می‌کنند. مواد مایع با قابلیت شکل پذیری و جریان یافتن در شبکه‌های ریز ، کاربردهای زیادی در صنعت پیدا کرده‌اند.

گاز

حالت فیزیکی مواد در شرایط فشار و درجه حرارت طبیعی ، بستگی به اندازه مولکولی و نیروهای فی‌مابین آن دارد. اگر مقدار کمی از یک گاز ، در یک تانک نسبتا بزرگی قرار گیرد، مولکولهای آن با سرعت در سرتاسر تانک پخش می‌شوند. پخش سریع مولکولهای گاز دلالت بر آن می‌کند که نیروهای موجود فی‌مابین مولکولها ، بمراتب ضعیفتر از انرژی جنبشی آن است و از آنجایی که ممکن است مقدار کمی از یک گاز در سرتاسر تانک یافت شود، نشان دهنده آن است که مولکولهای گاز باید نسبتا از هم فاصله گرفته باشند. بنابراین گازها شکل و حجمشان بستگی به ظرفی دارد که در آن جای دارند.

در حالت گازی ، مولکولها آزادانه به اطراف حرکت کرده و با یکدیگر و نیز با دیواره ظرف برخورد می‌کنند. فاصله مولکولها در حالت گازی در حدود چند ده برابر فاصله آنها در حالت مایع و جامد است. اگر در یک ظرف نوشابه پلاستیکی را بسته و آنرا متراکم کنید و سپس آنرا با آب پر کرده و دوباره سعی کنید که آنرا متراکم کنید، در حالت اول بعلت فاصله زیاد بین مولکولی در گاز ، متراکم کردن سنگین‌تر و سخت‌تر صورت می‌گیرد، در صورتی که در حالت دوم چنین نیست.

پلاسما

پلاسما حالت چهارمی از ماده است که دانش امروزی نتوانسته آنها را جزو سه حالت دیگر پندارد و مجبور شده آنرا حالت مستقلی به حساب آورد. این ماده با ماهیت محیط یونیزه ، ترکیبی از یونهای مثبت و الکترون با غلظت معین می‌باشد که مقدار الکترونها و یونهای مثبت در یک محیط پلاسما تقریبا برابر است و حالت پلاسمای مواد ، تقریبا حالت شبه خنثایی دارد. پدیده‌های طبیعی زیادی از جمله آتش ، خورشید ، ستارگان و غیره در رده حالت پلاسمایی ماده قرار می‌گیرند.

پلاسما شبیه به گاز است، ولی مرکب از ذرات باردار متحرکی به نام یون است. یونها بشدت تحت تاثیر نیروهای الکتریکی و مغناطیسی قرار می‌گیرند. مواد طبیعی در حالت پلاسما عبارتند از انواع شعله ، بخش خارجی جو زمین ، اتمسفر ستارگان ، بسیاری از مواد موجود در فضای سحابی و بخشی از دم ستاره دنباله‌دار و شفقهای قطبی شمالی. نمایش خیره کننده از حالت پلاسمایی ماده است که در میدان مغناطیسی جریان می‌یابد.

بد نیست بدانید که دانش امروزی حالات دیگری از جمله برهمکنش ضعیف و قوی هسته‌ای را نیز در دسته‌بندیها بعنوان حالات پنجم و ششم ماده بحساب می‌آورد که از این حالات در توجیه خواص نکلئونهای هسته ، نیروهای هسته‌ای ، واکنش های هسته‌ای و در کل ((فیزیک ذرات بنیادی استفاده می‌شود.

ساختمان گاز متان ، یک گاز طبیعی

چگال بوز-اینشتین

حالت پنجم با نام ماده چگال بوز-اینشتین (Booze-Einstein condensate) که در سال ۱۹۹۵ کشف شد، در اثر سرد شدن ذراتی به نام بوزون‌ها (Bosons) تا دماهایی بسیار پایین پدید می‌آید. بوزون‌های سرد در هم فرومی‌روند و ابر ذره‌ای که رفتاری بیشتر شبیه یک موج دارد تا ذره‌های معمولی ، شکل می‌گیرد. ماده چگال بوز-اینشتین شکننده‌ است و سرعت عبور نور در آن بسیار کم است.

چگال فرمیونی

حالت تازه هم ماده چگال فرمیونی (Fermionic condensate) است. "دبورا جین" (Deborah Jin) از دانشگاه کلورادو که گروهش در اواخر پاییز ۱۳۸۲ ، موفق به کشف این شکل تازه ماده شده‌ است، می‌گوید: "وقتی با شکل جدیدی از ماده روبرو می‌شوید، باید زمانی را صرف شناخت ویژگیهایش کنید. آنها این ماده تازه را با سرد کردن ابری از پانصدهزار اتم پتاسیم با جرم اتمی 40 تا دمایی کمتر از یک میلیونیم درجه بالاتر از صفر مطلق پدیدآوردند. این اتمها در چنین دمایی بدون گرانروی جریان می‌یابند و این ، نشانه ظهور ماده‌ای جدید بود. در دماهای پایین‌تر چه اتفاقی میافتد؟ هنوز نمیدانیم."

ماده چگال فرمیونی بسیار شبیه ماده چگال بوز-اینشتین (BEC) است. ذرات بنیادی و اتمها در طبیعت می‌توانند به شکل بوزون یا فرمیون باشند. یکی از تفاوتهای اساسی میان آنها حالتهای کوانتومی مجاز برای ذرات است. تعداد زیادی بوزون می‌توانند در یک حالت کوانتومی باشند ، مثلا انرژی ، اسپین و ... آنها یکی باشد ، اما مطابق اصل طرد پائولی ، دو فرمیون نمی‌توانند همزمان حالتهای کوانتومی یکسان داشته باشند.

برای همین ، مثلا در آرایش اتمی ، الکترونها که فرمیون هستند، نمی‌توانند همگی در یک تراز انرژی قرار گیرند.در هر اوربیتال تنها دو الکترون که اسپین‌های متفاوت داشته باشند، جا می‌گیرد و الکترونهای بعدی باید به اوربیتال دیگری با انرژی بالاتر بروند. بنابراین اگر فرمیونها را سرد کنیم و انرژی آنها را بگیریم ، ابتدا پایین‌ترین تراز انرژی پر می‌شود ، اما ذره بعدی باید به ترازی با انرژی بالاتر برود.

وجود ماده چگال فرمیونی همانند ماده چگال یوز- اینشتین سالها قبل پیش‌بینی شده و خواص آن محاسبه شده بود ، اما رسیدن به دمای نزدیک به صفر مطلق که برای تشکیل این شکل ماده لازم است تاکنون ممکن نشده بود. هر دو از فرورفتن اتمها در دماهایی بسیار پایین ساخته می‌شوند. اتمهای BEC بوزون ‌هستند و اتمهای ماده چگال فرمیونی ، فرمیون.

جامدات

جامد یک ماده متراکم است ، که توسط اتمهای نزدیک به هم که الگوی منظمی به نام شبکه را به وجود می آورند ایجاد می شود. این اتمها با نیروهایی قوی در کنار یکدیگر قرار گرفته اند ، که فقط اجازه حرکات خفیفی را می دهد . سختی یک جامد به آرایش و حرکت اتمهای آن بستگی دارد . مثلاَ عنصر کربن هم به شکل نرمی به نام گرافیت ، و هم به شکل یکی از سخت ترین جامدات روی زمین ، یعنی الماس، وجود دارد. تفاوت این دو شکل در آرایش اتمهایشان است.

کشسانی

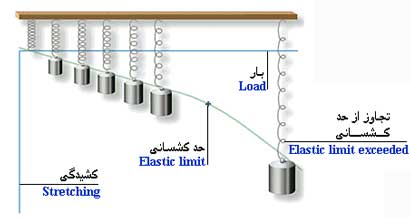
کشسانی قابلیت یک جامد در بازگشتن به شکل اولیه خود پس از کشیده شدن یا هر تغییر شکل دیگر است . مثلاَ یک فنر کشیده شده پس از رها شدن به سرعت به شکل اولیه خود باز می گردد . اما اگر آن را بیش از حد بکشیم ، به شکل اولیه خود باز نمی گردد و حتی ممکن است پاره شود . با نزدیک شدن به حد شکستن ، فنر کشسانی خود را از دست می دهد و تغییر شکل دائمی می یابد . این حد ، حد کشسانی نامیده می شود.

فنر کشسان فنر به کشیده شدن ادامه می دهد تا اینکه به حد کشسانی برسد.

قانون هوک

قانون هوک می گوید که نیروی اعمال شده به یک ماده با مقدار کشیده شدن متناسب است . یعنی مثلاَ اگر نیروی کشش وارد بر یک فنر را دو یا سه برابر کنید ، دو یا سه برابر بیشتر کشیده خواهد شد . اما این قانون پس از رسیدن به حد کشسانی ماده ، دیگر برقرار نیست. رابرت هوک پس از آتش سوزی بزرگ لندن در سال 1666 ، بازرس ارشد شهر لندن شد . او برای کمک به بازرسانی شهر ، رابطه بین کشسانی (الاستیسیته) مواد و نیروهای اعمال شده به انها را مورد تحقیق قرار داد. (بر گرفته از مکانیک سیالات شیمز)